Wie verkleineren sich die Kästchen zum Fluchtpunkt hin?

Frage zum perspektivischen Zeichnen und Verkürzen

Frage: Ich habe das Beispiel mit dem Schachbrett genommen, wo ich Perspektive mit einem Fluchtpunkt angewendet habe.
Gibt es eine Regel wie sich die Kästchen zum Fluchtpunkt verkleinern in der Breite? Und die Figuren? Oder ist das alles nur so Schätzung?

Antwort: Da die perspektivische Zeichnung auf physikalischen Gesetzen beruht, kann man sich tatsächlich alles berechnen.

In den Abbildungen (eine Vergrößung ist verlinkt) habe ich versucht die Perspektive und die Verkürzung für Quadrate zu verdeutlichen.

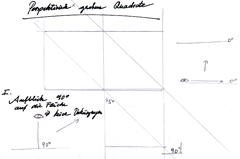In der oberen Zeichnung 1. Aufblick 90 Grad auf die Fläche wird zunächst die einfache Aufsicht von oben dargestellt:
Die Winkel der Quadrate haben 90 Grad. Ihre Diagonalen 45 Grad.

In der unteren Zeichnung 2. die Fläche wird perspektivisch gesehen wird die Verkürzung der selben Kästchen im Raum wiedergegeben.

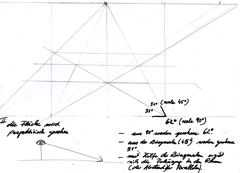Vorgehensweise zur Berechnung der Verkürzung:

Zunächst wurde nur die untere waagerechte Linie und die Horizontlinie mit Fluchtpunkt eingezeichnet.

Danach wurden die Abstände der Kästchen wie beim Aufblick auf der unteren waagerechten Linie eingezeichnet und mit dem Fluchtpunkt verbunden, so dass die in den Raum flüchtenden Linien entstanden.

Wahlweise wurde nun ein Winkel zwischen der unteren waagerechten Linie und einer Flucht abgemessen: Aus realen 90 Grad wurden perspektivische 62 Grad. Daraus folgt: Aus realen 45 Grad der Diagonalen werden perspektivische 31 Grad Diagonalen, die man nun einzeichnet.
Anmerkung: Also einfach den Winkel halbieren. In der Geometrie macht man dann - glaube ich - mit dem Zirkel drei Kreise und verbindet die Schnittpunkte.

Aus der Diagonale ergibt sich die Verkürzung der Kästchen: Durch die Diagonalen und die entstehenden Schnittpunkte kann man nun die weiteren Waagerechten (Parallelen) zum Fluchtpunkt hin einzeichnen. Schritt für Schritt erhält man so die sich korrekt verkürzende Quadrate.

Die Proportionen der Figuren lassen sich dann aus den gesehen Kästchen aus verschiedenen Ebenen erarbeiten.

Mehr zu diesem Thema:

<< Zur Galerie der OnlineMalschule von Kunst-Malerei.info

Zeichen- und Maltipps >>Fragen und Antworten